11/15/2025
Recently, I published my bachelor’s thesis on Rust memory management in neural networks at KTH. Fundamentally, I looked at how the borrow checker allocated memory and how we can rewrite certain sections to allocate more to the stack and less to the heap for optimal performance.
At the end of the report, I gave some ideas on how we could optimize this further by using macros and const generics. This is now implemented in version 2 of Micrograd-rs.
I wanted to write this blog post to discuss the new implementations in version 2 and expand on the questions that people had during my presentation. Think of it as a bachelor’s thesis director’s commentary.
If you are looking for the code, you can find it HERE.
I want to use this section as a little refresher or a summary on Micrograd-rs.
Micrograd-rs is a Rust rewrite of Micrograd, a minimalist
autograd engine by Andrej Karpathy. The goal of Micrograd-rs is to
increase our understanding of Rust’s memory allocation and discuss the
benefits/tradeoffs of the language. The main limitation was that it had
to be syntactically and computationally similar to Micrograd; note that
we disregard the syntax comparison for the second version. Micrograd has
two files for its program: the nn.py, which deals with the
neural network declaration and forward pass, and engine.py,
which is the autograd engine. We have followed the same convention for
our program and will call it the neural network and the autograd engine,
respectively.
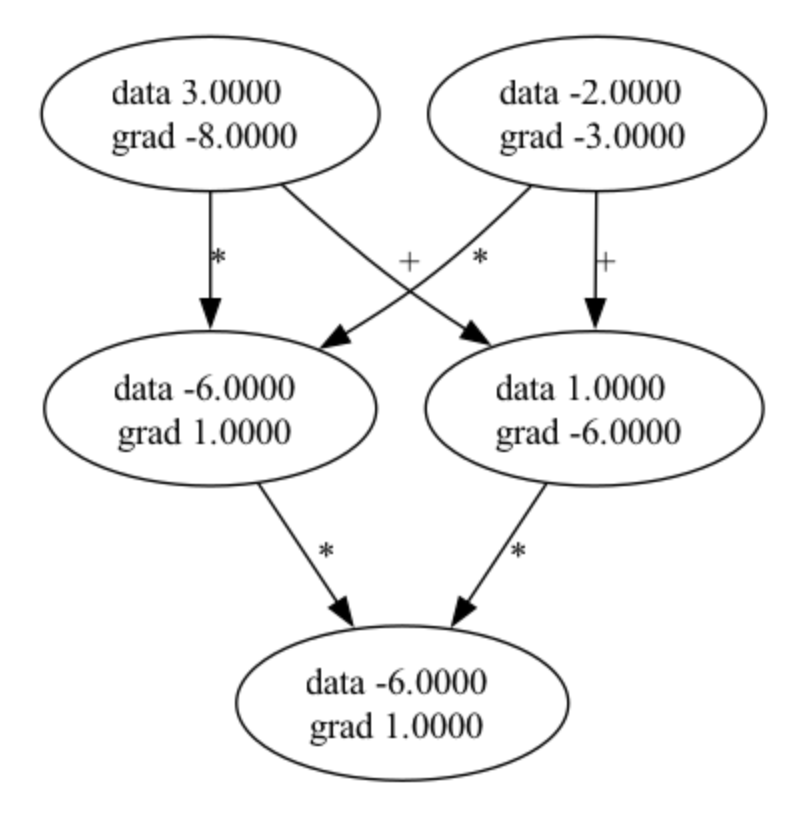
We can prove with the two images below that it is computationally identical to Micrograd. The code for these pictures can be found in the repository.
IMAGE GRAPH


On top of that, Micrograd-rs is able to do more complex tasks, such as non-linear classification. This is shown with the make moons example shown below:
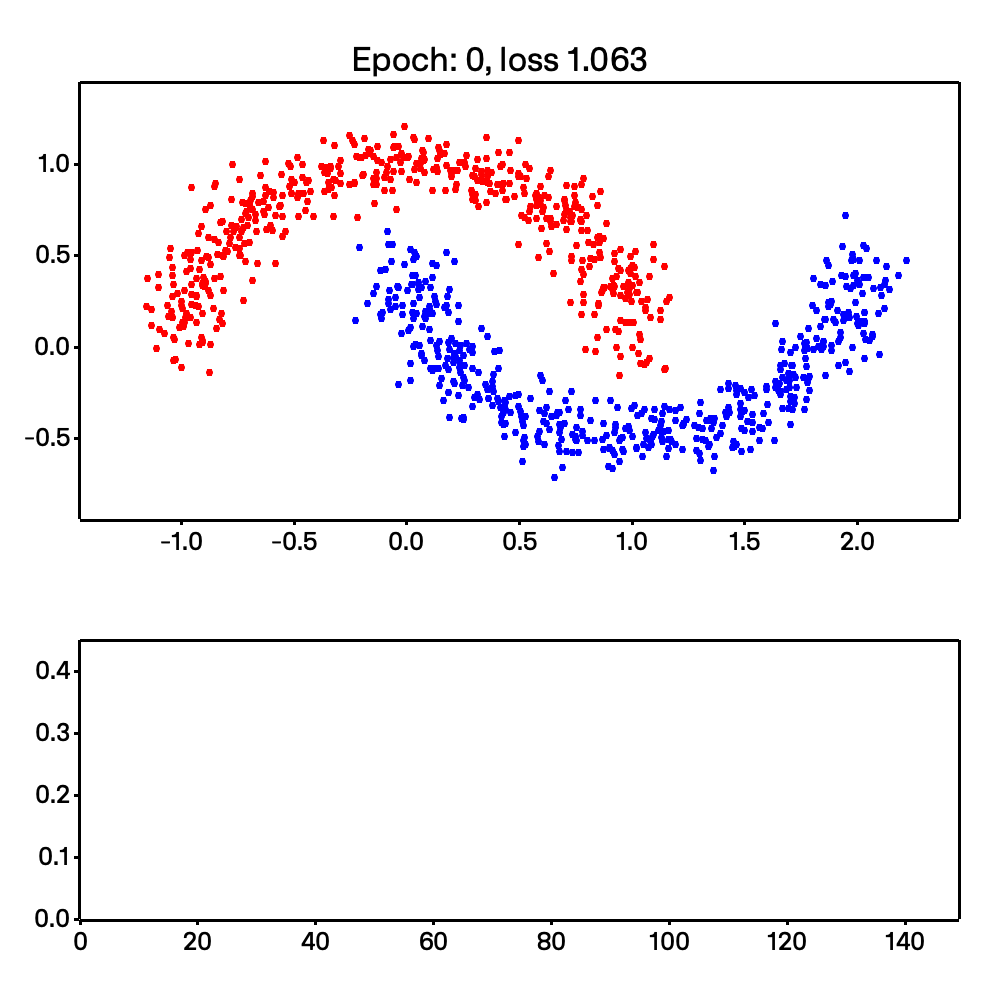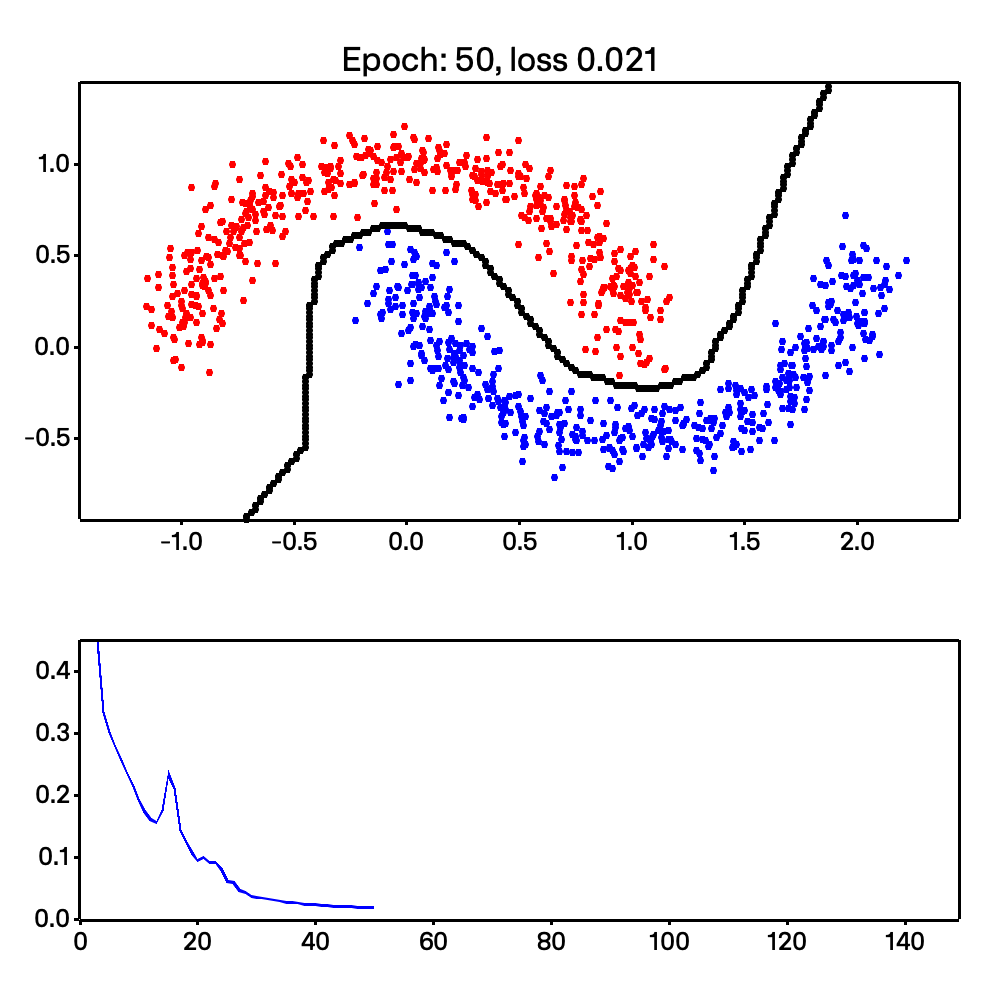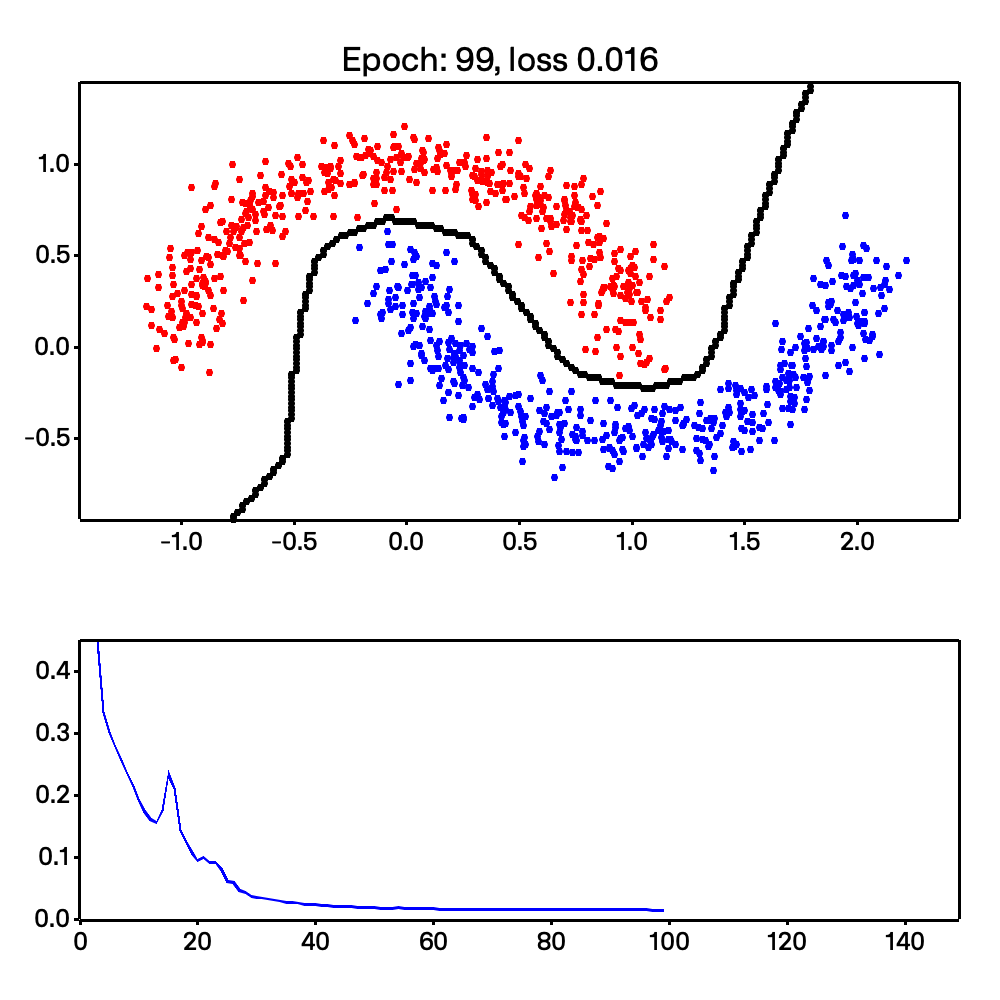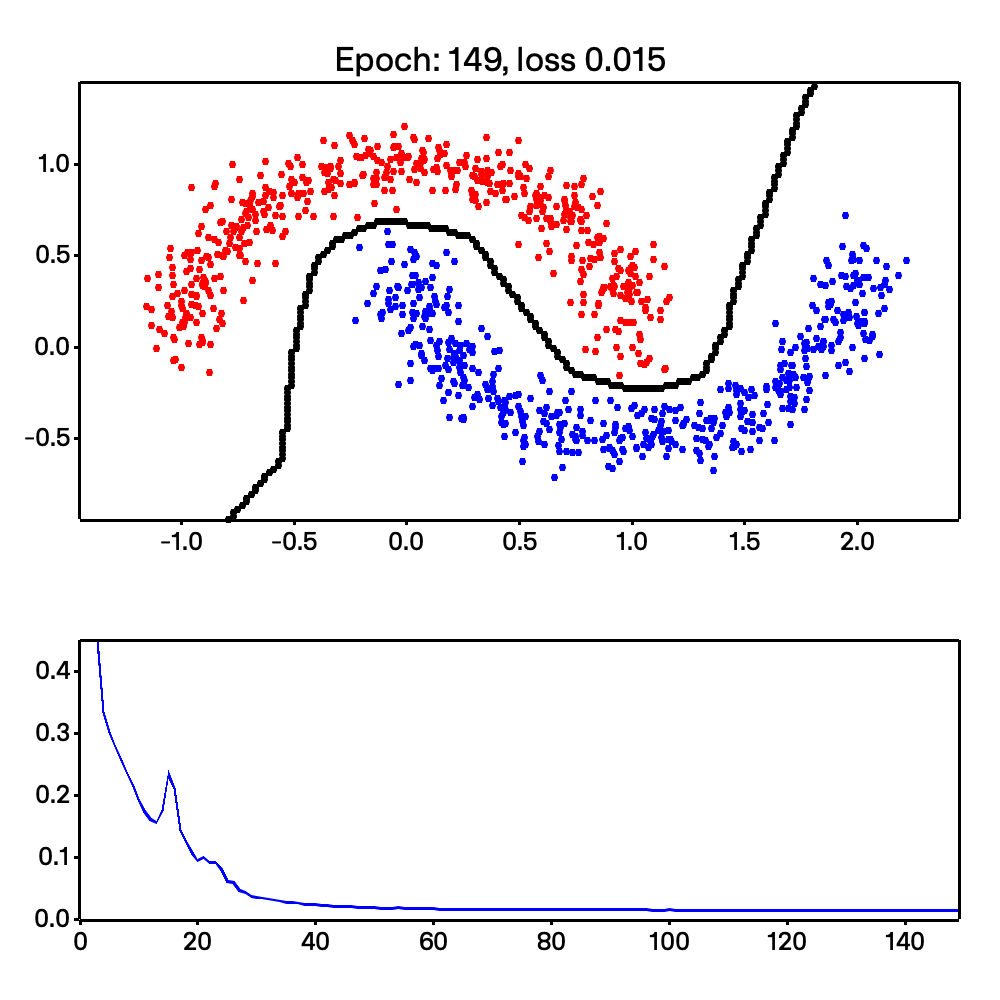
Looking at the code, we are able to easily calculate the stack and heap size due to Rust’s compile-time type checking. This section was inspired by chapter 2 of Jon Gjengset’s Rust for Rustaceans book. Read my thesis or the book for a deeper understanding of how I arrived here.
When we look at our memory allocation, we get the following for our neural network.
Note that the 24 bytes are allocated to the stack since our vector
datatypes need 3 words for their pointers; we assume a 64-bit system.
The rest of the equation is heap-allocated. is the memory
that is heap allocated for our
Value struct. It is
effectively the datatype that deals with our autograd engine.
You could probably notice a problem here; our entire program is effectively heap-allocated. Fundamentally, our issue is our choice of datatype for our neural network, or to be more specific, our overutilization of vectors. This is mainly caused by our requirement to be syntactically similar ot Python, which gives us little to no power to use Rustś strengths in our implementation. The improvements we implemented and further work will be discussed below.
I am going to break down each major improvement in Micrograd-rs below, similar to my thesis.
The obvious first step is to allocate more of our neural network to
the stack by implementing const generics for our neural network structs.
This means we have to give each Neuron the number of
neurons in the next layer. Because of this, we also need to pass this
through to our Layer struct, so it effectively has two
const generics as its input, the current (and next layer’s) number of
neurons. This effectively removes all heap-allocated vector, but the
total number of layers in our network is static. Effectively, what it
does is rewrite our equation to the following:
All of which is stack allocated, we will remove the total layer limit in a later section.
Now it might become obvious that we should probably remove the
Neuron struct and instead do our calculations using matrix
multiplication and addition. Since the neurons in our layer all have the
same activation function, it also removes l - 1 number of
bytes. While we do this, we will also change our nonlin to
an enum, which will still has 1 byte as its size. By removing the
Neuron, we can rewrite our MLP equation to the
following:
Note, we still have two Rc<T> in our weights and
bias, so we still will have Value be heap allocated.
However, for the rest, it’s simply stack allocated.
While we were at it, so to speak, we also rewrote parameters to be an
iterator yielding immutable references to Value, removing
the need for us to copy. It therefore does not allocate anything to the
heap or stack.
Now, the biggest issue we face is the fact that our MLP
is static. Thankfully, the Rust developers have already thought about a
problem like this and created the procedural macro; more specifically,
the function-like macros. Effectively, how they work is that they take a
token stream input, in our case, the number of layers, and automatically
generate the boilerplate needed for us. This allows us to generate an
MLP at runtime with the size needed for our task at hand,
using the command mlp!(x); where x is the number
of layers you need. We can also make our procedural macro generate only
const generics, allowing our neural network to be completely stack
allocated. This makes our function go back from a static size to a
flexible one, shown below:
This was probably the hardest part of the second version, and I am very surprised how well it works. I had to make a new Rust crate just for this macro, but I am very proud of it. Hopefully, I can use something similar to make our tensor arrays instead of vectors for the third version.
The first thing that was looked at for the next version of enigne.rs
is the Value and Values struct that was used.
Note that from now on, we will call it ValueData. The first
(kinda stupid) field that can be removed is the UUID
package. When I wrote my thesis, I was unaware that
Rc<T> has a pointer comparison function, which is now
obvious in retrospect; this removes 16 bytes from our
ValueData. Secondly, I also rewrote the op field to instead
use a static string, which is stored in the read-only data section of
the compiled binary executable. This removes 3 words, or 24 bytes, from
the stack. With these small changes in mind, we now allocate 48 bytes to
the stack instead of 88. Since our largest data type is 8 bytes, we can
tell that this is aligned and no padding is needed.
Another factor that I did, that actually added bytes to our struct,
was to remove the RefCell<T> encapsulation of
ValueData and instead only encapsulate data and grad. This added 16
bytes to our system, but removed unnecessary properties in op, prev, and
_backwards. Our main benefits here are in terms of memory efficiency and
removing the potential issue of runtime crashes, as when a process looks
at our Value struct, it has to lock the struct, allowing
other processes, for example, not to be able to look at the grad field
while another process looks at the data field. Long story short, it
isolates the specific fields that require interior mutability,
Note that since we still have Rc<T>, as we need
multiple owners for our data, our entire ValueData struct
is still heap allocated. So for our Value struct, we
allocate 1 word to the stack and the entire ValueData to
the heap. For our ValueData, we now only allocate 64 bytes as explained
previously.
On top of rewriting our value struct, we have also added new
operations and new declarative macros to remove boilerplate. As was
discussed in the Neural Network section, we have now removed the
individual Neuron struct and now do our operations on the
|Layer| struct. This means we needed to add a couple of new operators
that do matrix addition, multiplication, and multiplication + addition.
Since we still haven’t added any support for tensors, which I think I
will work on in the next version of this project, we need to go over
each item in the matrix, ie, element-wise. We solved this with
array::from\_fn package in the Rust standard library, to
keep our functional nature.. Note that since it is element-wise, the
operation is quite expensive; therefore, for speedup, we also created a
matmul\_add to allow us to also add our bias to every
operation, while we iterate over the list. Since we also deal with const
generics, we have to slightly change our input arguments, and since we
know basic linear algebra, we will know exactly how large the output
vector will be.
Because of this change, we also had to rewrite our activation functions to work similarly element-wise. This was a quick and small rewrite. However, we have rewritten it as an enum, which allocates 1 byte (unpadded) and 4 bytes (padded) to the stack.
As mentioned before, we also added declarative macros to remove as much boilerplate as possible; however, it did not yield any major benefits to our line count. This could probably be improved further, but it’s a topic for the next version.
In short, this version of Micrograd-rs is the version I wish I could
have written for my thesis. I believe it uses the strength of Rust to
show how a theoretical framework could utilise Rust to maximize the
performance we can gain by focusing on stack allocation rather than
having to deal with pointers. Now I do not want to make any statements
that this is of use ot anyone, instead I want this to be a kind of
bookmark for my future research into this topic. As long as the
Rc<T> component is in the Value struct,
I assume this is of no use to anyone, besides myself. I guess it is
simply here to increase my understanding of the Rust programming
language.
Also note that the changes made in Micrograd-rs v2 are noticeably faster too. Using our make_moons datasets, I have seen speedups of over 10x. I guess that’s what happens when you write a bad implementation and compare it to an implementation that actually uses the strength of the language at hand.
Micrograd fundamentally uses scalar values in its weights. Rewriting
the program to use tensors instead would make the program actually be
useful for real applications. If we want to continue our original focus,
on stack allocation, the datatype required could potentially be
generated using procedural macros similar to our MLP. I
don’t believe the operations within engine.rs would be
difficult to generate using procedural macros based on the generated
datatype.
This feature is very connected to the previous Tensor-based computation feature. This feature simply asks us to implement more operations and activation functions to make it possible to implement tests such as MNIST. This is more of a quality-of-life feature.
As part of my rewrite, Micrograd-rs sadly gained 3 more packages, but
as stated before, the UUID crate was deleted. If we were
able to rewrite or include the packages in our implementation, it could
potentially be possible to remove the standard library and make a
minimalist binary. This is a major rewrite that I will put off until I
am 100% certain that the approach I’m using is optimal, and to be fair,
this sounds more like another thesis. So I believe I will pursue it when
that becomes relevant.
This future work is not really relevant to Micrograd-rs, but instead
is relevant to the original goal of my thesis. Originally, I wanted to
show that neural networks are memory safe by using Rust; however, since
the Rust implementation requires RefCell, I was unable to
prove it using a Rust. Therefore, I want to do something similar by
first rewriting Micrograd in Haskell and then in Agda to formally prove
the correctness of neural networks. I have already written some simple
proofs in Agda, but as this is a major project it is perhaps also
another thesis.